Bryan Caplan is an optimist. He thinks that economists do many errors in estimating GDP (overall well-being). He is right in the sense that we are missing many dimensions of welfare improvements in the last half-century (see here, here and here). These errors in measurements lead us to hold incorrectly pessimistic views (such as those of Robert Gordon). However, Prof. Caplan seems to argue (I may be wrong) that all measurements problems and errors are greater than zero. In other words, they all cut in favor of omitting things. There are no reasons to believe this. Many measurement problems with GDP data cut the other way – in favor of adding too much (so that the true figures are lower than the reported ones).
Here are two errors of importance (which are in no way exhaustive): household output and adjustments for household size.
Household Output
From the 1910s to the 1940s, married women began to enter moderately the workforce. This trickle became a deluge thereafter. National GDP statistics are really good at capturing the extra output they were hired to produce. However, national GDP statistics cannot net out the production that was foregone: household output.
A married woman in 1940 did produce something: child-rearing, house chores, cooking, allowing the husband to specialize in his work. That output had a value. Once offered the chance to work, married women thought the utility generated from producing “home outputs” was inferior to the utility generated from “market work”. However, the output that is measured is only related to market work. Women entered the labor force and everything they produced was considered a net addition to GDP. In reality, any economist worth his salt is aware that the true improvement in well-being is equal to the increased market output minus the forsaken house output. Thus, in a transition from a “male-labor force” to a “mixed labor force”, you are bound to overestimate output increases.
How big of an issue is this? Well, consider this paper from 1996 in Feminist Economics. In that paper, Barnet Wagman and Nancy Folbre calculate output in both the “household” and “market” sectors. They find that even very small changes in the relative size of these sectors alter growth rates by substantial margins. Another example, which I discussed in this blog post based on articles in the Review of Income and Wealth, is that when you make the adjustment over four decades of available Canadian data, you can find that one quarter of the increase in living standards is eliminated by the proper netting out of the value of non-market output. These are sizable measurement errors that cut in the opposite direction as the one hypothesized by prof. Caplan (and in favor of people like prof. Gordon).
Household Size
Changes in household sizes also create overestimation problems. Larger households have more economies of scale to exploit than smaller households so that an income of $10,000 per capita in a household of six members is superior in purchasing power than an income of $10,000 per capita in a single-person household. If, over time, you move from large households to small households, you will overestimate economic growth. In an article in the Scottish Journal of Political Economy, I showed that making adjustments for household sizes over time yields important changes in growth rates between 1890 and 2000. Notice, in the table below, that GDP per adult equivalent (i.e. GDP per capita adjusted for household size) is massively different than GDP per capita. Indeed, the adjusted growth rates are reduced by close to two-fifths of their original values over the 1945-2000 period and by a third over the 1890 to 2000 period. This is a massive overestimation of actual improvements in well-being.
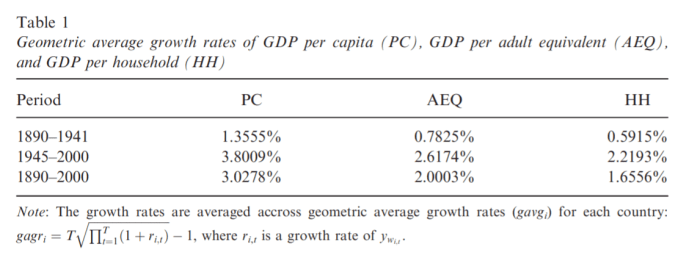
A large overestimation
If you assemble these two factors together, I hazard a guess that growth rates would be roughly halved (there is some overlap between the two so that we cannot simply sum them up as errors to correct for – hence my “guess”). This is not negligible. True, there are things that we are not counting as Prof. Caplan notes. We ought to find a way to account for them. However, if they simply wash out the overestimation, the sum of errors may equal zero. If so, those who are pessimistic about the future (and recent past) of economic growth have a pretty sound case. Thus, I find myself unable to share Prof. Caplan’s optimism.
Reblogged this on Utopia – you are standing in it!.
[…] but boy were they good: “Interwar US inequality data are deeply flawed” and “Not all GDP measurement errors are greater than zero!” Dr Geloso focused most of his time on publishing academic […]